5.2. Relationship of Pressure, Volume, Amount, and Temperature

Dinor Dhanabala; Sandra Fraley; Gordon Lake

Chapter 5: Gases and Introduction to Gas Laws

5.2. Relationship of Pressure, Volume, Amount, and Temperature

Learning Objectives

By the end of this section, you will be able to:

Identify the mathematical relationships between the various properties of gases

During the seventeenth and especially eighteenth centuries, driven both by a desire to understand nature and a quest to make balloons in which they could fly (Figure 5.2.1 ), a number of scientists established the relationships between the macroscopic physical properties of gases, that is, pressure, volume, temperature, and amount of gas.

This figure includes three images. Image a is a black and white image of a hydrogen balloon apparently being deflated by a mob of people. In image b, a blue, gold, and red balloon is being held to the ground with ropes while positioned above a platform from which smoke is rising beneath the balloon. In c, an image is shown in grey on a peach-colored background of an inflated balloon with vertical striping in the air. It appears to have a basket attached to its lower side. A large stately building appears in the background. — **Figure 5.2.1:** In 1783, the first **(a)** hydrogen-filled balloon flight, **(b)** manned hot air balloon flight, and **(c)** manned hydrogen-filled balloon flight occurred. When the hydrogen-filled balloon depicted in **(a)** landed, the frightened villagers of Gonesse reportedly destroyed it with pitchforks and knives. The launch of the latter was reportedly viewed by 400,000 people in Paris.

Pressure and Temperature: Amontons’s Law

Imagine filling a rigid container attached to a pressure gauge with gas and then sealing the container so that no gas may escape. If the container is cooled, the gas inside likewise gets colder and its pressure is observed to decrease. Since the container is rigid and tightly sealed, both the volume and number of moles of gas remain constant. If we heat the sphere, the gas inside gets hotter (Figure 5.2.2) and the pressure increases.

In the first diagram to the left, a rigid spherical container of a gas to which a pressure gauge is attached at the top is placed in a large beaker of water, indicated in light blue, atop a hot plate. The needle on the pressure gauge points to the far left on the gauge. The diagram is labeled “low P” above and “hot plate off” below. The second similar diagram also has the rigid spherical container of gas placed in a large beaker from which light blue wavy line segments extend from the top of the liquid in the beaker. The beaker is situated on top of a slightly reddened circular area. The needle on the pressure gauge points straight up, or to the middle on the gauge. The diagram is labeled “medium P” above and “hot plate on medium” below. The third diagram also has the rigid spherical container of gas placed in a large beaker in which bubbles appear near the liquid surface and several wavy light blue line segments extend from the surface out of the beaker. The beaker is situated on top of a bright red circular area. The needle on the pressure gauge points to the far right on the gauge. The diagram is labeled “high P” above and “hot plate on high” below. — **Figure 5.2.2:** The effect of temperature on gas pressure: When the hot plate is off, the pressure of the gas in the sphere is relatively low. As the gas is heated, the pressure of the gas in the sphere increases.

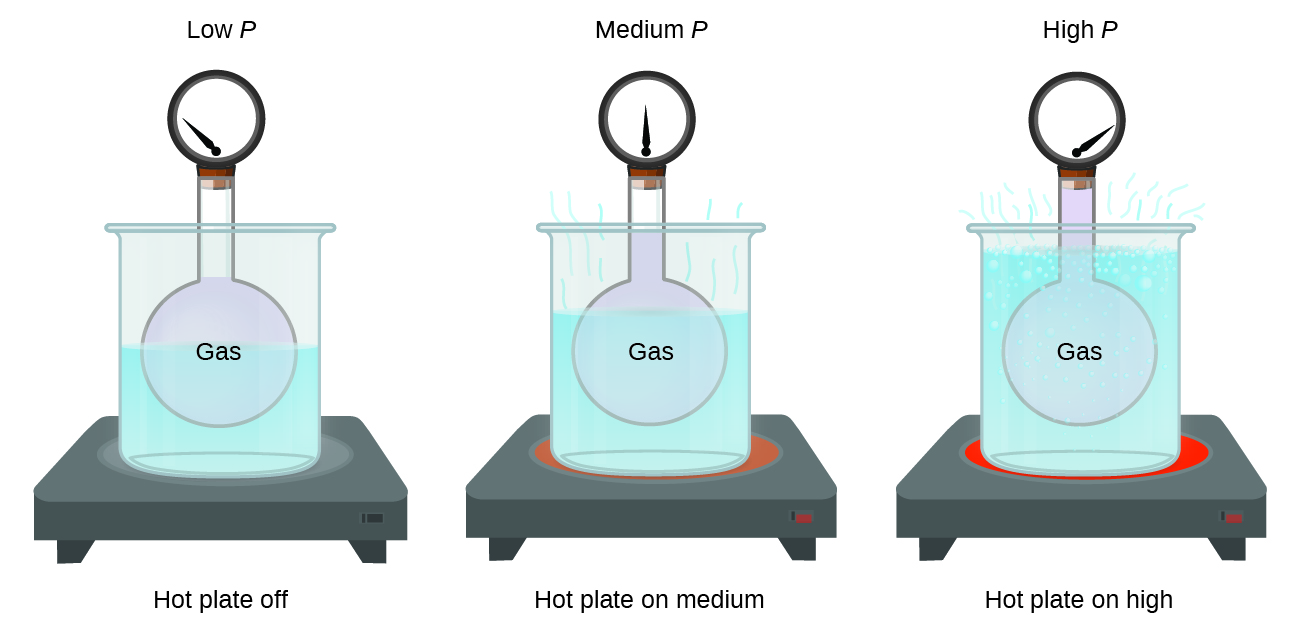
Guillaume Amontons was the first to empirically establish the relationship between the pressure and the temperature of a gas (~1700), and Joseph Louis Gay-Lussac determined the relationship more precisely (~1800). Because of this, the P–T relationship for gases is known as either Amontons’s law or Gay-Lussac’s law. Under either name, it states that the pressure of a given amount of gas is directly proportional to its temperature on the kelvin scale when the volume is held constant. Mathematically, this can be written:

P \propto T,

where ∝ means “is proportional to”.

Volume and Temperature: Charles’s Law

If we fill a balloon with air and seal it, the balloon contains a specific amount of air at atmospheric pressure, let’s say 1 atm. If we put the balloon in a refrigerator, the gas inside gets cold and the balloon shrinks (although both the amount of gas and its pressure remain constant). If we make the balloon very cold, it will shrink a great deal, and it expands again when it warms up.

Link to learning

This video (https://www.youtube.com/watch?v=ZgTTUuJZAFs) shows how cooling and heating a gas causes its volume to decrease or increase, respectively.

These examples of the effect of temperature on the volume of a given amount of a confined gas at constant pressure are true in general: The volume increases as the temperature increases, and decreases as the temperature decreases.

Volume and Pressure: Boyle’s Law

If we partially fill an airtight syringe with air, the syringe contains a specific amount of air at constant temperature, say 25 °C. If we slowly push in the plunger while keeping temperature constant, the gas in the syringe is compressed into a smaller volume and its pressure increases; if we pull out the plunger, the volume increases and the pressure decreases. This example of the effect of volume on the pressure of a given amount of a confined gas is true in general. Decreasing the volume of a contained gas will increase its pressure, and increasing its volume will decrease its pressure. In fact, if the volume increases by a certain factor, the pressure decreases by the same factor, and vice versa. Volume-pressure data for an air sample at room temperature are graphed in (Figure 5.2.3.).

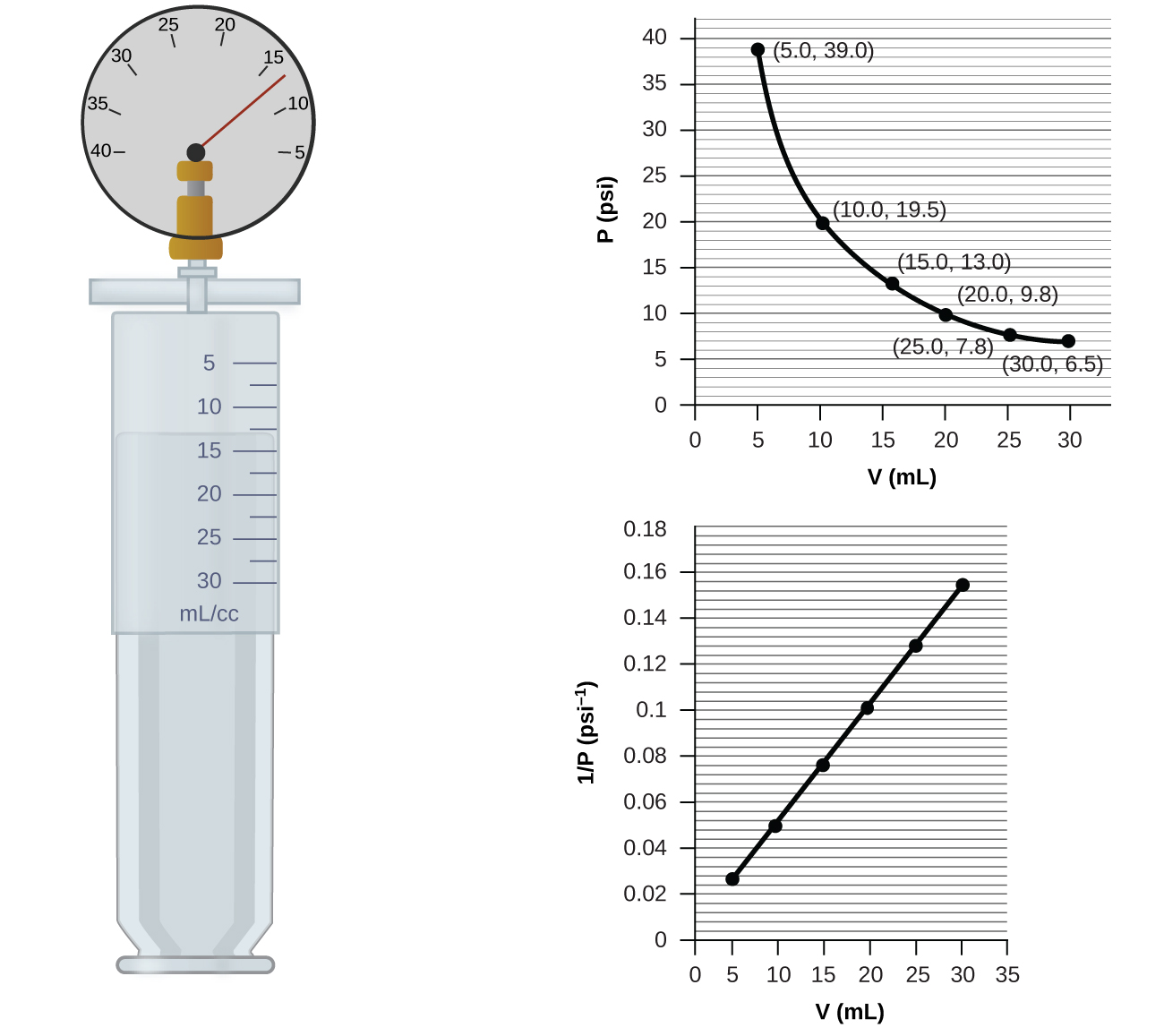
This figure contains a diagram and two graphs. The diagram shows a syringe labeled with a scale in m l or c c with multiples of 5 labeled beginning at 5 and ending at 30. The markings halfway between these measurements are also provided. Attached at the top of the syringe is a pressure gauge with a scale marked by fives from 40 on the left to 5 on the right. The gauge needle rests between 10 and 15, slightly closer to 15. The syringe plunger position indicates a volume measurement about halfway between 10 and 15 m l or c c. The first graph is labeled “V ( m L )” on the horizontal axis and “P ( p s i )” on the vertical axis. Points are labeled at 5, 10, 15, 20, and 25 m L with corresponding values of 39.0, 19.5, 13.0, 9.8, and 6.5 p s i. The points are connected with a smooth curve that is declining at a decreasing rate of change. The second graph is labeled “V ( m L )” on the horizontal axis and “1 divided by P ( p s i )” on the vertical axis. The horizontal axis is labeled at multiples of 5, beginning at zero and extending up to 35 m L. The vertical axis is labeled by multiples of 0.02, beginning at 0 and extending up to 0.18. Six points indicated by black dots on this graph are connected with a black line segment showing a positive linear trend. — **Figure 5.2.3:** When a gas occupies a smaller volume, it exerts a higher pressure; when it occupies a larger volume, it exerts a lower pressure (assuming the amount of gas and the temperature do not change). Since P and V are inversely proportional, a graph of 1/P vs. V is linear.

Unlike the P–T and V–T relationships, pressure and volume are not directly proportional to each other. Instead, P and V exhibit inverse proportionality: Increasing the pressure results in a decrease of the volume of the gas. Mathematically this can be written:

P α 1 / V

or P_{1} V_{1} = P_{2} V_{2}

The relationship between the volume and pressure of a given amount of gas at constant temperature was first published by the English natural philosopher Robert Boyle over 300 years ago. It is summarized in the statement now known as Boyle’s law: The volume of a given amount of gas held at constant temperature is inversely proportional to the pressure under which it is measured.

Example

A sample of gas has a volume of 15.0 mL at a pressure of 13.0 psi. Determine the pressure of the gas at a volume of 7.5 mL.

Solution

From Boyle’s law, we know that the product of pressure and volume (PV) for a given sample of gas at a constant temperature is always equal to the same value. Therefore we have P₁V₁ = k and P₂V₂ = k which means that P₁V₁ = P₂V₂.

Using P₁ and V₁ as the known values 13.0 psi and 15.0 mL, P₂ as the pressure at which the volume is unknown, and V₂ as the unknown volume, we have:

P_{1} V_{1} = P_{2} V_{2} or 13.0 psi \times 15.0 mL = P_{2} \times 7.5 mL

Solving:

P_{2} = \frac{13.0 psi \times 15.0 mL}{7.5 mL} = 26 psi

Breathing and Boyle’s Law

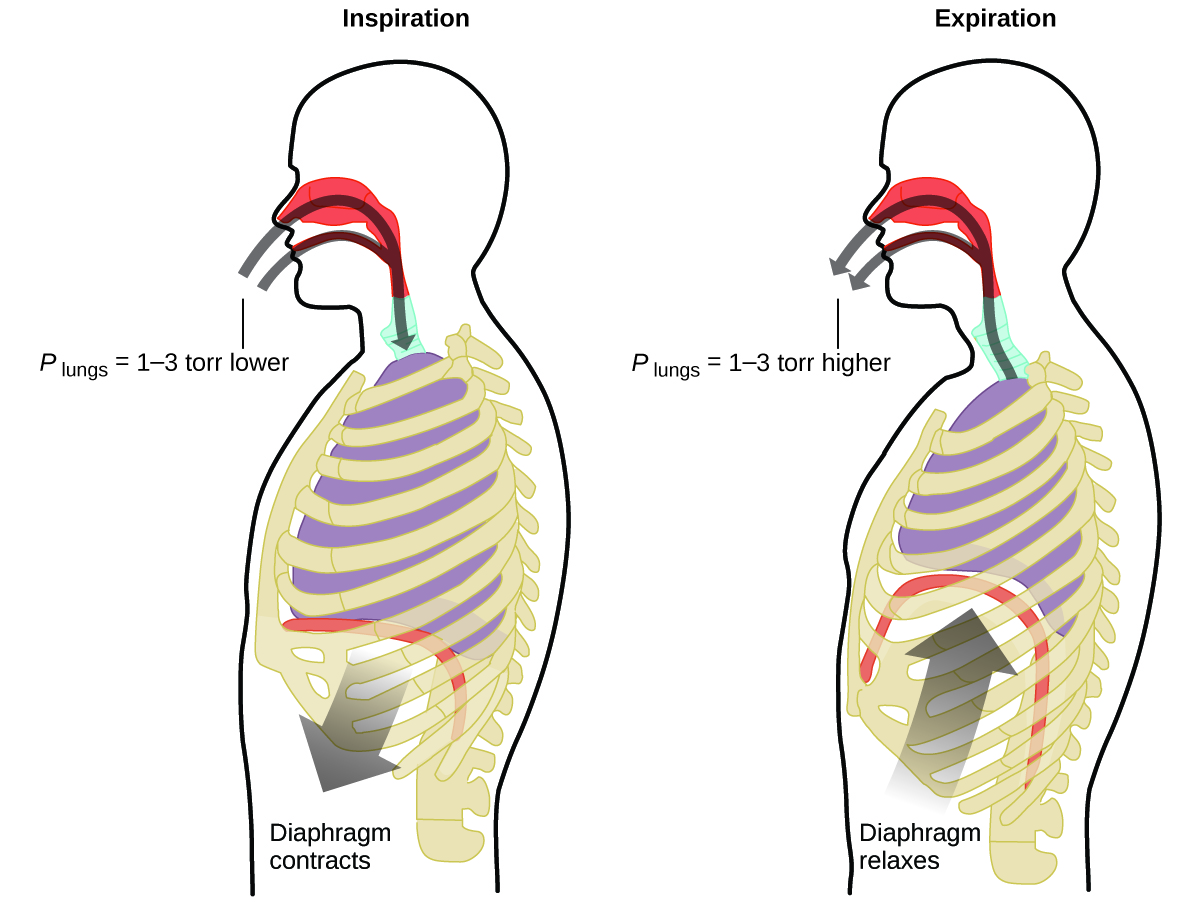
What do you do about 20 times per minute for your whole life, without break, and often without even being aware of it? The answer, of course, is respiration, or breathing. How does it work? It turns out that the gas laws apply here. Your lungs take in gas that your body needs (oxygen) and get rid of waste gas (carbon dioxide). Lungs are made of spongy, stretchy tissue that expands and contracts while you breathe. When you inhale, your diaphragm and intercostal muscles (the muscles between your ribs) contract, expanding your chest cavity and making your lung volume larger. The increase in volume leads to a decrease in pressure (Boyle’s law). This causes air to flow into the lungs (from high pressure to low pressure). When you exhale, the process reverses: Your diaphragm and rib muscles relax, your chest cavity contracts, and your lung volume decreases, causing the pressure to increase (Boyle’s law again), and air flows out of the lungs (from high pressure to low pressure). You then breathe in and out again, and again, repeating this Boyle’s law cycle for the rest of your life (Figure 5.2.4).

This figure contains two diagrams of a cross section of the human head and torso. The first diagram on the left is labeled “Inspiration.” It shows curved arrows in gray proceeding through the nasal passages and mouth to the lungs. An arrow points downward from the diaphragm, which is relatively flat, just beneath the lungs. This arrow is labeled “Diaphragm contracts.” At the entrance to the mouth and nasal passages, a label of P subscript lungs equals 1 dash 3 torr lower” is provided. The second, similar diagram, which is labeled “Expiration,” reverses the direction of both arrows. Arrows extend from the lungs out through the nasal passages and mouth. Similarly, an arrow points up to the diaphragm, showing a curved diaphragm and lungs reduced in size from the previous image. This arrow is labeled “Diaphragm relaxes.” At the entrance to the mouth and nasal passages, a label of P subscript lungs equals 1 dash 3 torr higher” is provided. — **Figure 5.2.4:** Breathing occurs because expanding and contracting lung volume creates small pressure differences between your lungs and your surroundings, causing air to be drawn into and forced out of your lungs.

Example in everyday life

The Interdependence between Ocean Depth and Pressure in Scuba Diving

Whether scuba diving at the Great Barrier Reef in Australia (shown in Figure 5.2.5) or in the Caribbean, divers must understand how pressure affects a number of issues related to their comfort and safety.

This picture shows colorful underwater corals and anemones in hues of yellow, orange, green, and brown, surrounded by water that appears blue in color. — **Figure 5.2.5:** Scuba divers, whether at the Great Barrier Reef or in the Caribbean, must be aware of buoyancy, pressure equalization, and the amount of time they spend underwater, to avoid the risks associated with pressurized gases in the body. (credit: Kyle Taylor)

Pressure increases with ocean depth, and the pressure changes most rapidly as divers reach the surface. The pressure a diver experiences is the sum of all pressures above the diver (from the water and the air). Most pressure measurements are given in units of atmospheres, expressed as “atmospheres absolute” or ATA in the diving community: Every 33 feet of salt water represents 1 ATA of pressure in addition to 1 ATA of pressure from the atmosphere at sea level. As a diver descends, the increase in pressure causes the body’s air pockets in the ears and lungs to compress; on the ascent, the decrease in pressure causes these air pockets to expand, potentially rupturing eardrums or bursting the lungs. Divers must therefore undergo equalization by adding air to body airspaces on the descent by breathing normally and adding air to the mask by breathing out of the nose or adding air to the ears and sinuses by equalization techniques; the corollary is also true on ascent, divers must release air from the body to maintain equalization. Buoyancy, or the ability to control whether a diver sinks or floats, is controlled by the buoyancy compensator (BCD). If a diver is ascending, the air in his BCD expands because of lower pressure according to Boyle’s law (decreasing the pressure of gases increases the volume). The expanding air increases the buoyancy of the diver, and she or he begins to ascend. The diver must vent air from the BCD or risk an uncontrolled ascent that could rupture the lungs. In descending, the increased pressure causes the air in the BCD to compress and the diver sinks much more quickly; the diver must add air to the BCD or risk an uncontrolled descent, facing much higher pressures near the ocean floor. The pressure also impacts how long a diver can stay underwater before ascending. The deeper a diver dives, the more compressed the air that is breathed because of increased pressure: If a diver dives 33 feet, the pressure is 2 ATA and the air would be compressed to one-half of its original volume. The diver uses up available air twice as fast as at the surface.

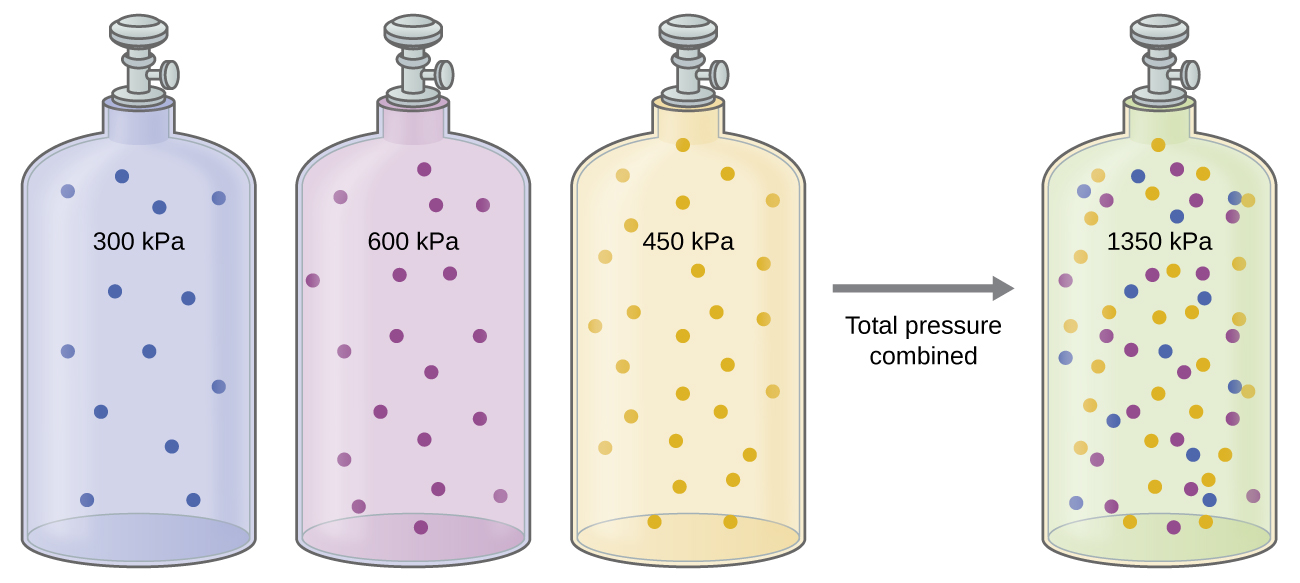
The Pressure of a Mixture of Gases: Dalton’s Law

Unless they chemically react with each other, the individual gases in a mixture of gases do not affect each other’s pressure. Each individual gas in a mixture exerts the same pressure that it would exert if it were present alone in the container (Figure 5.2.6.). The pressure exerted by each individual gas in a mixture is called its partial pressure. This observation is summarized by Dalton’s law of partial pressures: The total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases:

P_{T o t a l} = P_{A} + P_{B} + P_{C} + … = Σ_{i} P_{i}

In the equation P_Total is the total pressure of a mixture of gases, P_A is the partial pressure of gas A; P_B is the partial pressure of gas B; P_C is the partial pressure of gas C; and so on.

This figure includes images of four gas-filled cylinders or tanks. Each has a valve at the top. The interior of the first cylinder is shaded blue. This region contains 5 small blue circles that are evenly distributed. The label “300 k P a” is on the cylinder. The second cylinder is shaded lavender. This region contains 8 small purple circles that are evenly distributed. The label “600 k P a” is on the cylinder. To the right of these cylinders is a third cylinder. Its interior is shaded pale yellow. This region contains 12 small yellow circles that are evenly distributed. The label “450 k P a” is on this region of the cylinder. An arrow labeled “Total pressure combined” appears to the right of these three cylinders. This arrow points to a fourth cylinder. The interior of this cylinder is shaded a pale green. It contains evenly distributed small circles in the following quantities and colors; 5 blue, 8 purple, and 12 yellow. This cylinder is labeled “1350 k P a.” — **Figure 5.2.6:** If equal-volume cylinders containing gas A at a pressure of 300 kPa, gas B at a pressure of 600 kPa, and gas C at a pressure of 450 kPa are all combined in the same-size cylinder, the total pressure of the mixture is 1350 kPa.

Here is an example of this concept, but dealing with fraction calculations.

The Pressure of a Mixture of Gases A gas mixture used for anesthesia contains 2.83 mol oxygen, O₂, and 8.41 mol nitrous oxide, N₂O. The total pressure of the mixture is 192 kPa.

(a) What are the mole fractions (proportion) of O₂ and N₂O?

(b) What are the partial pressures of O₂ and N₂O?

Solution

Given that mole fraction is:

$X_{A} = \frac{n_{A}}{n_{T o t a l}}$ and the partial pressure is P_A = X_A

$\times$ P_Total.

For O₂,

X_{O_{2}} = \frac{n_{O_{2}}}{n_{T o t a l}} = \frac{2.83 mol}{(2.83 + 8.41) mol} = 0.252

and

$P_{O_{2}} = X_{O_{2}} \times P_{T o t a l} = 0.252 \times 192 kPa = 48.4 kPa$

For N₂O,

X_{N_{2} O} = \frac{n_{N_{2} O}}{n_{Total}} = \frac{8.41 mol}{(2.83 + 8.41) mol} = 0.748

and

$P_{N_{2} O} = X_{N_{2} O} \times P_{Total} = 0.748 \times 192 kPa = 144 kPa$

Key Concepts and Summary

Recalling that gas pressure is exerted by rapidly moving gas molecules and depends directly on the number of molecules hitting a unit area of the wall per unit of time, we see that the KMT conceptually explains the behavior of a gas as follows:

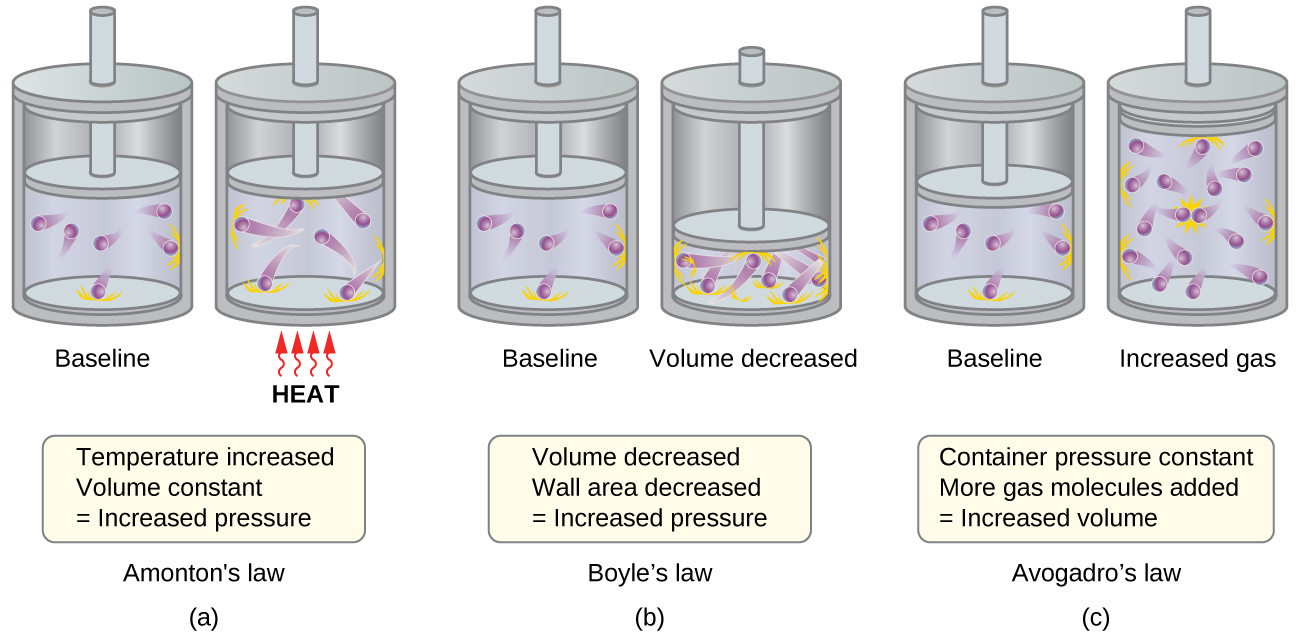
Amontons’s law. If the temperature is increased, the average speed and kinetic energy of the gas molecules increase. If the volume is held constant, the increased speed of the gas molecules results in more frequent and more forceful collisions with the walls of the container, therefore increasing the pressure (Figure 5.2.7.(a)).
Charles’s law. If the temperature of a gas is increased, a constant pressure may be maintained only if the volume occupied by the gas increases. This will result in greater average distances traveled by the molecules to reach the container walls, as well as increased wall surface area. These conditions will decrease the both the frequency of molecule-wall collisions and the number of collisions per unit area, the combined effects of which balance the effect of increased collision forces due to the greater kinetic energy at the higher temperature.
Boyle’s law. If the gas volume is decreased, the container wall area decreases and the molecule-wall collision frequency increases, both of which increase the pressure exerted by the gas (Figure 5.2.7.(b)).
Avogadro’s law. At constant pressure and temperature, the frequency and force of molecule-wall collisions are constant. Under such conditions, increasing the number of gaseous molecules will require a proportional increase in the container volume in order to yield a decrease in the number of collisions per unit area to compensate for the increased frequency of collisions (Figure 5.2.7(c)).
Dalton’s Law. Because of the large distances between them, the molecules of one gas in a mixture bombard the container walls with the same frequency whether other gases are present or not, and the total pressure of a gas mixture equals the sum of the (partial) pressures of the individual gases.

This figure shows 3 pairs of pistons and cylinders. In a, which is labeled, “Charles’s Law,” the piston is positioned for the first cylinder so that just over half of the available volume contains 6 purple spheres with trails behind them. The trails indicate movement. Orange dashes extend from the interior surface of the cylinder where the spheres have collided. This cylinder is labeled, “Baseline.” In the second cylinder, the piston is in the same position, and the label, “Heat” is indicated in red capitalized text. Four red arrows with wavy stems are pointing upward to the base of the cylinder. The six purple spheres have longer trails behind them and the number of orange dashes indicating points of collision with the container walls has increased. A rectangle beneath the diagram states, “Temperature increased, Volume constant equals Increased pressure.” In b, which is labeled, “Boyle’s Law,” the first, baseline cylinder shown is identical to the first cylinder in a. In the second cylinder, the piston has been moved, decreasing the volume available to the 6 purple spheres to half of the initial volume. The six purple spheres have longer trails behind them and the number of orange dashes indicating points of collision with the container walls has increased. This second cylinder is labeled, “Volume decreased.” A rectangle beneath the diagram states, “Volume decreased, Wall area decreased equals Increased pressure.” In c, which is labeled “Avogadro’s Law,” the first, baseline cylinder shown is identical to the first cylinder in a. In the second cylinder, the number of purple spheres has changed from 6 to 12 and volume has doubled. This second cylinder is labeled “Increased gas.” A rectangle beneath the diagram states, “At constant pressure, More gas molecules added equals Increased volume.” — **Figure 5.2.7:** **(a)** When gas temperature increases, gas pressure increases due to increased force and frequency of molecular collisions. **(b)** When volume decreases, gas pressure increases due to increased frequency of molecular collisions. (c) When the amount of gas increases at a constant pressure, volume increases to yield a constant number of collisions per unit wall area per unit time.

Key Equations

P ∝ T
P ∝ 1/V
P₁V₁ = P₂V₂
P_Total = P_A+ P_B + P_C + …

Glossary

Amontons’s law: (also, Gay-Lussac’s law) pressure of a given number of moles of gas is directly proportional to its kelvin temperature when the volume is held constant

Boyle’s law: volume of a given number of moles of gas held at constant temperature is inversely proportional to the pressure under which it is measured

Charles’s law: volume of a given number of moles of gas is directly proportional to its kelvin temperature when the pressure is held constant

Dalton’s law of partial pressures: total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases

partial pressure: pressure exerted by an individual gas in a mixture

License and attributions:

Chemistry: Atoms first, Second edition, 2019, Flowers, P. et al. License: CC BY 4.0. Located at https://openstax.org/books/chemistry-atoms-first-2e/pages/8-2-relating-pressure-volume-amount-and-temperature-the-ideal-gas-law

License

Icon for the Creative Commons Attribution 4.0 International License

BIO130: Introduction to Physiology Copyright © 2024 by Dinor Dhanabala; Sandra Fraley; and Gordon Lake is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.